NG-Task 24 (Alternative Uses for ICESat-2 and Other Laser Altimeter Data)

Safety of navigation depends on our knowledge of seabed and its features, and, as such, any improvements in deriving bathymetry for nautical chart updating are of major importance. Due to the limited available resources, it often takes years for hydrographic offices to re-survey an area. There are cases where charts have been compiled with data collected over a hundred years ago. 

Satellite derived bathymetry (SDB) from multispectral remote sensing has shown potential as a supplement to traditional surveys, particularly for mapping remote and shallow areas, due to its reduced cost and the absence of navigational risks in very shallow and unsurveyed areas. SDB has received significant attention since the 1970s and multiple algorithms have been developed. The ability to retrieve bathymetric information from SDB is based on the observed radiance as a function of wavelength and depth. The two most used band-ratio optimization approaches are those developed by Dierssen et al. (2003) (Equation 24-1), which uses a log-difference concept to derive bathymetry, and Stumpf et al. (2003), which uses the division between the observed radiance log values of two bands. 𝐿𝑜𝑏𝑠(𝜆𝑗) represents the observed radiance for each band, m0 the translation coefficient based on bottom return, and m1 the diffuse attenuation. Linear regression is applied to transform imagery values into depths.

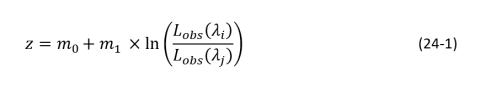
A main concern with SDB is that the accuracy of the method is not adequate for many coastal applications, including nautical charting.  One of the reasons may be that the conventional approaches assume that bottom type and water clarity are constant and negligible within the entire image, and consequently, a single (global) and linear model is performed. Researchers have investigated the use of a nonlinear model with the aim to improve the accuracy of the derived bathymetry. Recently, Freire (2017) developed an extended Dierssen model – the nonlinear case of Equation 24-2, based on that in Equation 24-1, tuning the ratio of natural logarithms for the reflectance value from different wavelengths. Parameters Lw(λj) and Lw(λi), represent the observed radiance over optically deep waters with no bottom contribution.

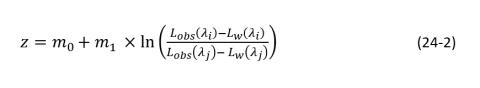
To address the spatial heterogeneity within a scene and with the aim to increase the accuracy and coverage of estimated depths, Juliane Affonso, under the supervision of Christos Kastrisios, Christopher Parish (Oregon State University), and Brian Calder, investigated the use of multi-temporal, non-linear techniques, and the segmentation of the scene, both horizontally and vertically, into smaller spatial units.  The idea of the spatial segmentation is based on the assumption that the magnitude of spatial heterogeneity is smaller (and possibly non-existent) in small regions, therefore we divide the image scene into smaller spatial units and calibrate the model within each segment. The individual models use the same algorithm but varying model parameters.

In the previous reporting period, the research team evaluated the performance of the extended Dierssen model in the Dry Tortugas, Florida. The system is solved with linear regression, however, due to the model not being linear, the final solution represents an approximated solution to the observation. Also, instead of two control points, at least four points are required for the extended Dierssen model solution. The process, implemented in the Python programming language, consists of the: (1) estimation of the initial vector, (2) Development of the Jacobian matrix, and (3) Minimization of the quadratic sum of the residuals. 

The preliminary results showed that the added parameters (which represent the observed radiance over optically deep waters with no bottom contribution in the extended Dierssen equation) result in better depth estimates compared to the traditional Dierssen and Stumpf models.

In this reporting period the research team further evaluated the extended Dierssen model and subsequently focused on the investigation of the spatial segmentation of the scene using six different segmentation approaches:

Horizontal Segmentation (Figure 24-4)  

1. Regular Segmentation
   This method divides the image scene into regular cells and provides the SDB solution within each cell. Two arbitrarily selected grid cell sizes are tested, one of 30 × 30 pixels and one of 150 × 150 pixels. Initially, the image is divided into the smaller square grids of 30 × 30 pixels; if a solution of the model cannot be derived due to insufficient control points within the grid cell, this is merged into the larger grid cell of 150 × 150 pixels.

2. Irregular Segmentation 

   1. Global-Local: The method begins with calibrating a single extended Dierssen model (“Global”), similarly to conventional approaches. Accordingly, the prediction residuals are calculated for the Global model (i.e., the difference between the Global model (𝑧𝑔𝑙𝑜𝑏𝑎𝑙) and the referenced depths (𝑧𝑟𝑒𝑓)) and the area is subdivided into classes/regions for the residual and depths (“Local”). A model is calibrated for each class using the training data points within each area.

   2. Depth Areas (DA): the image scene is segmented into depth areas of defined ranges and a model is calibrated within each depth area. When a small depth area does not contain the minimum necessary number of control points, it is merged and processed with same depth areas in different locations. For this work, depth areas are formed for every 5m, i.e., 0-5m, 5-10m, and so on.

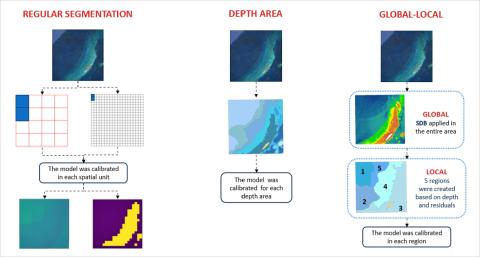
Figure 24-4. The horizontal segmentation workflow.

 
Vertical Segmentation  (Figure 24-5)
The vertical segmentation approach applies a piecewise regression to the band-ratio/depth to improve the accuracy in depths below the effective optical depth and to attempt the extraction of bathymetry beyond this point. To accomplish the vertical segmentation, the dataset was divided by depth, beginning with depth ranges of 5m which progressively decrease to 1m, and, given that enough control points exist, a model is calibrated for each subset of training data points. Based on the resulting RMSE, the best range selection provides the final bathymetry estimation. 
 

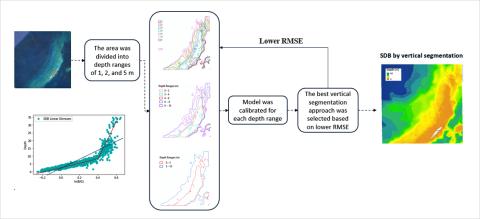
Figure 24-5. The vertical segmentation workflow.

 
Merged Segmentation
The merged segmentation approach is the combination of the horizontal and vertical segmentation methods. In detail, each spatial unit created with the above two irregular horizontal segmentation approaches is divided vertically into depth ranges of 1m for two merged approaches:

1. Global-Local by Depth Range (GLDR): spatial segments created in the Global-Local approach are vertically divided every 1 m. 

2. Depth Areas by Depth Range (DADR): spatial segments created in the Depth Area approach are divided into depth ranges every 1 m.

The methods were evaluated in Dry Tortugas - Loggerhead Key, west of Key West between the Gulf of Mexico and the Atlantic Ocean, and St. Thomas East End Reserve (STEER), U.S. Virgin Islands. In both sites, the use of the extended Dierssen model improved the accuracy compared to the traditional, simplified Dierssen model. In terms of the geographic approaches, all the investigated geographic approaches more accurately estimated depth compared to the widely used conventional band-ratio algorithms. Furthermore, the results suggest that the vertical segmentation of the scene (Vertical and DADR in Figure 24-6) allows for inferring bathymetry beyond the effective optical depth (10 m in the particular areas) which is the limit for depth estimation with the conventional approaches, thus increasing the coverage of the estimated SDB. Among all approaches, the vertical and DADR methods performed the best (Table 24-1). 
 
Table 24 -1. Comparison of results between geographic and conventional approaches.

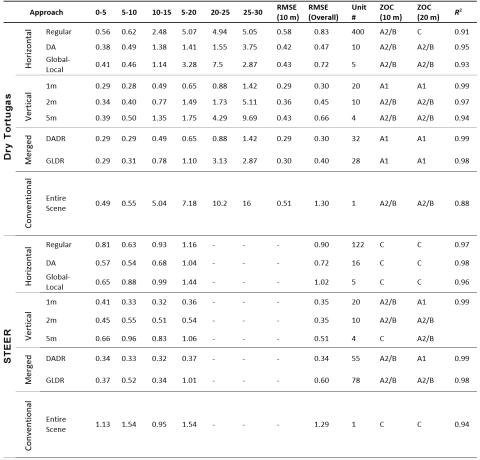
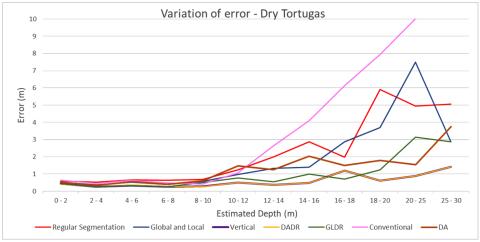
Figure 24-6. Performance of geographic models and conventional SDB approach in Dry Tortugas. The error variation is represented in depth ranges of 2 m.

 
The geographic models provided significant improvements in depth estimation however, a few limitations and concerns exist. First, there is increased need for control points compared to the global models due to the greater number of spatial units for which a model should be calibrated. Furthermore, the geographic models consist of multiple steps compared to the conventional method, with a subsequent increase in the processing time. Lastly, all vertical approaches (5m, 2m, 1m) performed better than the global methods, and particularly that of the 1m, however, the segmentation results in discontinuities between the individual linear regression models of each depth range (Figure 24-7). It is part of future work to investigate whether the vertical segmentation approach indeed results in a substantial accuracy increase, as this work demonstrated, as well as the optimal bin size for improving accuracy and coverage without overtraining the model and losing its predictive capabilities.
 

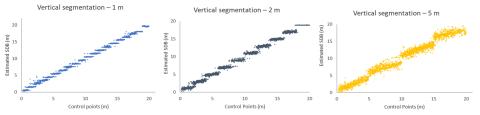
Figure 24-7. The quantized appearance in different depth ranges – 1m depth range (left), 2m (center), and 5m (right).

 
References

Caballero I., Stumpf, R. P., 2019 Retrieval of nearshore bathymetry from Sentinel-2A and 2B satellites in South Florida coastal waters. Estuarine, Coastal and Shelf Science, Vol.226, 2019, 106277. 

Caballero I., Stumpf, R. P., 2020. Atmospheric correction for satellite-derived bathymetry in the Caribbean waters: from a single image to multi-temporal approaches using Sentinel-2A/B. Optics Express, Vol.28, No. 8/13. 

Dierssen, H. M., Zimmerman, R. C., Leathers R. A., Downes, T. V. and Davis, C. O. (2003). Ocean color remote sensing of seagrass and bathymetry in the Bahamas Banks by high-resolution airborne imagery. Limnol. and Oceanogr. 48: 444–455.

Freire, R.R., 2017. Evaluating Satellite Derived Bathymetry in Regard to Total Propagated Uncertainty, Multi-Temporal Change Detection, and Multiple Non-Linear Estimation. University of New Hampshire.

Stumpf, R. P., Holderied, K. and Sinclair, M. 2003. Determination of water depth with high-resolution satellite imagery over variable bottom types, Limnol. Oceanogr. 48: 547–556.

Su, H, Liu H., Wang L., Filippi A. M., Heyman W. D., Beck R. A., 2013.Geographically Adaptive Inversion Model for Improving Bathymetric Retrieval From Satellite Multispectral Image. IEEE Transactions on Geoscience and Remote Sensing, vol. 52, no. 1, pp. 465-476, doi: 10.1109/TGRS.2013.2241772.